Why

Mathematics is truly fascinating, seemingly chaotic behavior once broken down to bits, bytes and variables starts making sense not only helps us to not only predict the future behavior and utilize those predictions to our applications; but the journey of solving a problem provides us with tools for solving the next problem blocking our way.

To put it poetically, the real maths is the tools we made along the way.

This series is an attempt to ignite/reignite my/your love for mathematics which is lost in this academe-bureaucratic prison of gate keeping.

Why should you care?

Mathematics like any intellectual endeavour requires a way of thinking to be developed in user such that arbitrary problems can be solved. Those skills can be re-used in other intellectual endeavors like programming, 3D-modelling, drawing etc.

To quote this post itself

seemingly chaotic behavior once broken down to bits, bytes and variables starts making sense.

Now where can be this skill be used?

In my life

  • Programming
  • Designing Gadgets (post coming soon)
  • Martial Arts (yes, not joking)

It’s like lifting weights seemingly specific but the skills you acquire turnout to be pretty functional. Brain is like body if not trained atrophies into Minimum Viable Product which should be the starting point not the end goal.

P: The Problem

A bead of mass $ m $ is resting on uniform string of length $ l $ anchored on 2 points distance $ d $ apart leveled horizontally such that $ d \lt l $, the coefficient of friction(static and kinetic) between string and bead is $ \mu $.

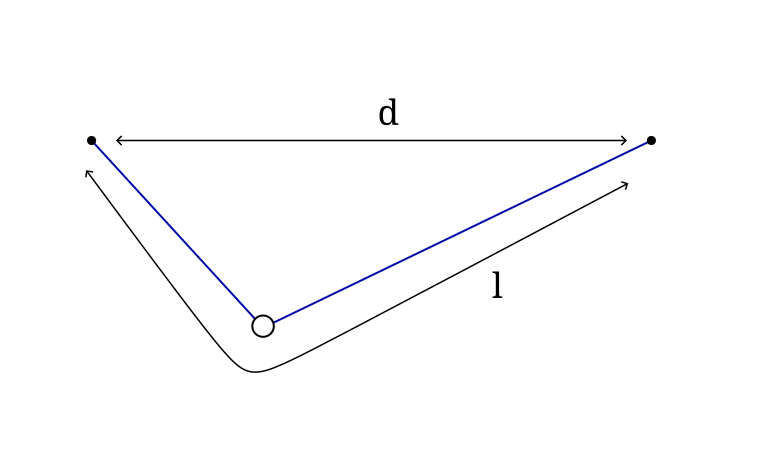
Problem Illustration, Fig. 1

  1. Resting position of bead, if the bead is release from the position just beneath the anchor when string is taught when.

    1. Bead is released pseudo-statically.
    2. Bead is released freely.

  2. From the resting position found from 1. if the anchors are accelerated upwards and stopped such that bead is propelled upwards find the equation that describes path taken by the bead. Let acceleration and time at which anchors are stopped be $ a $ and $ t $ respectively.

Solutions, might have symmetry so answers with respect to any of the anchors is

V: Variations

  1. Bead

    1. point sized bead
    2. Spherical bead sized comparable to $ d $ and $ l $.

  2. String

    1. Non-stiff string
    2. Stiff string

Solutions

  • P 1.1 V { 11.21, 12.21, 11.22, 12.22} (coming soon)
  • P 1.2 V { 11.21, 12.21, 11.22, 12.22} (coming soon)
  • P 2 V { 11.21, 12.21, 11.22, 12.22} (coming soon)